Abstract
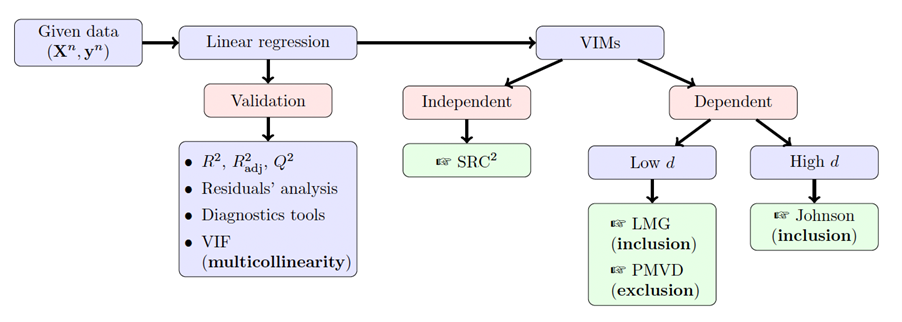
One of the most fundamental issues in many socio-environmental studies is the identification of causal effects and influential variables related to phenomena of interest. In the context of regression analysis, importance measures are effective tools for feature selection and model interpretation, allowing for the ranking of the most influential regressors. In particular, variance-based importance measures (VIMs) are a prominent topic in the field of statistics, as well as in the emerging field of global sensitivity analysis. This is due to their accessible interpretation as variance shares of the explained variable. This work focuses on the linear regression model and aims to provide an updated overview of the most well-founded methods, mainly from comparative analyses and numerical tests on various toy cases. The paper also addresses some of the practical challenges that arise, including the case of dependent inputs and high input dimensionality. The practical relevance of these tools is demonstrated through empirical studies on simulated data and public datasets. The Supplementary Material C also presents the use of VIMs in a classification context, specifically via the logistic linear regression model.
References
Achen, C. H. (1982). Interpreting and Using Regression. SAGE Publications.
Antoniadis, A., Lambert-Lacroix, S., & Poggi, J.-M. (2021). Random forests for global sensitivity analysis: A selective review. Reliability Engineering & System Safety, 206(107312).
Belsley, D., Kuh, E., & Welsch, R. (1980). Regression diagnostics: Identifying influential data and sources of collinearity. John Wiley & Sons, Inc.
Bénard, C., Biau, G., Veiga, S. D., & Scornet, E. (2022). SHAFF: Fast and consistent SHApley eFfect estimates via random Forests. In Proceedings of the 25th International Conference on Artificial Intelligence and Statistics (AISTATS) 2022, volume 151 of PMLR, Valencia, Spain.
Benoumechiara, N. & Elie-Dit-Cosaque, K. (2019). Shapley effects for sensitivity analysis with dependent inputs: bootstrap and kriging-based algorithms. ESAIM: Proceedings and Surveys, 65:266–293.
Bi, J. (2012). A review of statistical methods for determination of relative importance of correlated predictors and identifi- cation of drivers of consumer liking. Journal of Sensory Studies, 27:87–101.
Blanchard, J.-B. (2023). Sensitivity analysis with correlated inputs: comparison of indices for the linear case. International Journal for Uncertainty Quantification, 13:25–56.
Borgonovo, E. & Plischke, E. (2016). Sensitivity analysis: A review of recent advances. European Journal of Operational Research, 248:869–887.
Broto, B., Bachoc, F., & Depecker, M. (2020). Variance reduction for estimation of Shapley effects and adaptation to unknown input distribution. SIAM/ASA Journal on Uncertainty Quantification, 8:693–716.
Broto, B., Bachoc, F., Depecker, M., & Martinez, J.-M. (2019). Sensitivity indices for independent groups of variables. Mathematics and Computers in Simulation, 163:19–31.
Budescu, D. (1993). Dominance analysis: A new approach to the problem of relative importance of predictors in multiple regression. Psychological Bulletin, 114:542–551.
Chatterjee, S. & Price, B. (1977). Regression Analysis by Example. John Wiley & Sons, New York. Christensen, R. (1990). Linear models for multivariate, time series and spatial data. Springer-Verlag.
Clouvel, L. (2019). Uncertainty quantification of the fast flux calculation for a PWR vessel. Thèse de l’Université Paris- Saclay.
Clouvel, L., Mosca, P., Martinez, J., & Delipei, G. (2019). Shapley and Johnson values for sensitivity analysis of PWR power distribution in fast flux calculation. In M&C 2019, Portland, USA.
Da Veiga, S., Gamboa, F., Iooss, B., & Prieur, C. (2021). Basics and Trends in Sensitivity Analysis. Theory and Practice in R. SIAM.
Darlington, R. & Hayes, A. (2017). Regression analysis and linear models. The Guilford Press.
Deng, X., Yin, L., Peng, S., & Ding, M. (2015). An iterative algorithm for solving ill-conditioned linear least squares problems. Geodesy and Geodynamics, 6(6):453–459.
Fekhari, E., Iooss, B., Muré, J., Pronzato, L., & Rendas, J. (2023). Model predictivity assessment: incremental test-set selection and accuracy evaluation. In Salvati, N., Perna, C., Marchetti, S., & Chambers, R., editors, Studies in Theoretical and Applied Statistics, SIS 2021, Pisa, Italy, June 21-25, pages 315–347. Springer.
Feldman, B. (2000). The proportional value of a cooperative game. In Econometric Society World Congress 2000 Con- tributed papers, number 1140. Econometric Society.
Feldman, B. (2005). Relative importance and value. SSRN Electronic Journal.
Fox, J. & Monette, G. (1992). Generalized Collinearity Diagnostics. Journal of the American Statistical Association, 87(417):178–183.
Genizi, A. (1993). Decomposition of 𝑅2 in multiple regression with correlated regressors. Statistica Sinica, pages 407–420.
Grömping, U. (2006). Relative importance for linear regression in R: the Package relaimpo. Journal of Statistical Software, 17:1–27.
Grömping, U. (2007). Estimators of relative importance in linear regression based on variance decomposition. The American Statistician, 61(2).
Grömping, U. (2015). Variable importance in regression models. WIREs Comput Stat, 7(137-152).
Helton, J. (1993). Uncertainty and sensitivity analysis techniques for use in performance assesment for radioactive waste disposal. Reliability Engineering & System Safety, 42:327–367.
Helton, J., Johnson, J., Salaberry, C., & Storlie, C. (2006). Survey of sampling-based methods for uncertainty and sensitivity analysis. Reliability Engineering & System Safety, 91:1175–1209.
Hérin, M., Il Idrissi, M., Chabridon, V., & Iooss, B. (2022). Proportional marginal effects for sensitivity analysis with correlated inputs. In Proceedings of the 10th International Conference on Sensitivity Analysis of Model Output (SAMO 2022), Tallahassee, Florida, USA.
Hérin, M., Il Idrissi, M., Chabridon, V., & Iooss, B. (2024). Proportional marginal effects for global sensitivity analysis. SIAM/ASA Journal of Uncertainty Quantification, 12:667–692.
Il Idrissi, M., Chabridon, V., & Iooss, B. (2021a). Developments and applications of Shapley effects to reliability-oriented sensitivity analysis with correlated inputs. Environmental Modelling & Software, 143(105115).
Il Idrissi, M., Iooss, B., & Chabridon, V. (2021b). Mesures d’importance relative par décomposition de la performance de modèles de régression. In Actes des 52èmes Journées de Statistique de la Société Française de Statistique (SFdS), pages 497–502, Nice, France.
Iooss, B., Chabridon, V., & Thouvenot, V. (2022). Variance-based importance measures for machine learning model inter- pretability. In Actes du 23ème Congrès de Maîtrise des Risques et de Sûreté de Fonctionnement (𝜆𝜇23), Saclay, France. Institut pour la Maîtrise des Risques, URL: https://hal.science/IMDR/hal-03878431v1.
Iooss, B. & Clouvel, L. (2023). Une méthode d’approximation des effets de Shapley en grande dimension. In Actes des 54èmes Journées de Statistique de la Société Française de Statistique (SFdS), Brussels, Belgium, URL: https://hal.science/hal-04088622/document.
Iooss, B., Da Veiga, S., Janon, A., & Pujol, G. (2023). sensitivity: Global Sensitivity Analysis of Model Outputs. R package version 1.29.0.
Iooss, B. & Lemaître, P. (2015). A review on global sensitivity analysis methods. In Meloni, C. & Dellino, G., editors, Uncertainty management in Simulation-Optimization of Complex Systems: Algorithms and Applications, pages 101–122. Springer.
Iooss, B. & Prieur, C. (2019). Shapley effects for sensitivity analysis with dependent inputs: comparisons with Sobol’ indices, numerical estimation and applications. International Journal for Uncertainty Quantification, 9:493–514,.
James, G., Witten, D., Hastie, T., & Tibshirani, R. (2014). An introduction to statistical learning: With applications in R, 7th edition. Springer.
Johnson, J. (2000). A heuristic method for estimating the relative weight of predictor variables in multiple regression. Multivariate Behavioral Research, 35:1–19.
Johnson, J. & LeBreton, J. (2004). History and use of relative importance indices in organizational research. Organizational Research Methods, 7:238–257.
Johnson, R. (1966). The minimal transformation to orthonormality. Psychometrika, 31:61–66. Karch, J. (2020). Improving on Adjusted R-Squared. Collabra: Psychology, 6(1):1–11.
Kruskal, W. (1987). Relative importance by averaging over orderings. The American Statistician, 41:6–10. Kurowicka, D. & Cooke, R. (2006). Uncertainty analysis with high dimensional dependence modelling. Wiley.
Lepore, A., Palumbo, B., & Poggi, J.-M., editors (2022). Interpretability for Industry 4.0: Statistical and Machine Learning Approaches. Springer.
Lindeman, R. H., Merenda, P. F., & Gold, R. Z. (1980). Introduction to bivariate and multivariate analysis. Scott Foresman and Company, Glenview, IL.
Marrel, A., Iooss, B., Van Dorpe, F., & Volkova, E. (2008). An efficient methodology for modeling complex computer codes with Gaussian processes. Computational Statistics and Data Analysis, 52:4731–4744.
McCullagh, P. & Nelder, J. (1989). Generalized linear models. Chapman & Hall.
Molnar, C., Casalicchio, G., & Bischl, B. (2020). Interpretable machine learning - A brief history, state-of-the-art and challenges. In PKDD/ECML Workshops 2020, pages 417–431.
Nathans, L. L., Oswald, F. L., & Nimon, K. (2012). Interpreting multiple linear regression: a guidebook of variable importance. Practical assessment, research & evaluation, 17(9):n9.
Nimon, K. & Oswald, F. (2013). Understanding the results of multiple linear regression: Beyond standardized regression coefficients. Organizational Research Methods, 16:650–674.
Owen, A. (2014). Sobol’ indices and Shapley value. SIAM/ASA Journal on Uncertainty Quantification, 2:245–251.
Owen, A. & Prieur, C. (2017). On Shapley value for measuring importance of dependent inputs. SIAM/ASA Journal on Uncertainty Quantification, 5:986–1002.
Perez, D. (2022). An attempt of reproduction of sovacool et al.’s differences in carbon emissions reduction. EPJ Nuclear Science & Technology, 8:24.
Plischke, E., Rabitti, G., & Borgonovo, E. (2021). Computing Shapley effects for sensitivity analysis. SIAM/ASA Journal on Uncertainty Quantification, 9:1411–1437.
Razavi, S., Jakeman, A., Saltelli, A., Prieur, C., Iooss, B., Borgonovo, E., Plischke, E., Lo Piano, S., Iwanaga, T., Becker, W., Tarantola, S., Guillaume, J., Jakeman, J., Gupta, H., Melillo, N., Rabiti, G., Chabridon, V., Duan, Q., Sun, X., Smith, S., Sheikholeslami, R., Hosseini, N., Asadzadeh, M., Puy, A., Kucherenko, S., & Maier, H. (2020). The future of sensitivity analysis: An essential discipline for systems modelling and policy making. Environmental Modelling and Software, 137(104954).
Saltelli, A., Bammer, G., Bruno, I., Charters, E., Di Fiore, M., Didier, E., Espeland, W., Kay, J., Lo Piano, S., Mayo, D., Jr, R., Portaluri, T., Porter, T., Puy, A., Rafols, I., Ravetz, J., Reinert, E., Sarewitz, D., Stark, P., & Vineis, P. (2020). Five ways to ensure that models serve society: a manifesto. Nature, 582:482–484.
Saltelli, A., Chan, K., & Scott, E., editors (2000). Sensitivity analysis. Wiley Series in Probability and Statistics. Wiley. Shapley, L. (1953). A value for n-persons game. In Kuhn, H. & Tucker, A., editors, Contributions to the theory of games II, Annals of mathematic studies. Princeton University Press, Princeton, NJ.
Sobol’, I. (1993). Sensitivity estimates for non linear mathematical models. Mathematical Modelling and Computational Experiments, 1:407–414.
Song, E., Nelson, B., & Staum, J. (2016). Shapley effects for global sensitivity analysis: Theory and computation. SIAM/ASA Journal on Uncertainty Quantification, 4:1060–1083.
Sovacool, B., Schmid, P., Stirling, A., Walter, G., & MacKerron, G. (2020). Differences in carbon emissions reduction between countries pursuing renewable electricity versus nuclear power. Nature Energy, 5:928.
Thomas, D., Zumbo, B., Kwan, E., & Schweitzer, L. (2014). On johnson’s (2000) relative weigths method for assessing variable importance: A reanalysis. Multivariate Behavioral Research, 49:329–338.
Tonidandel, S. & LeBreton, J. M. (2015). Rwa web: A free, comprehensive, web-based, and user-friendly tool for relative weight analyses. Journal of Business and Psychology, 30:207–216.
Wagner, F. (2021). CO2 emissions of nuclear power and renewable energies: a statistical analysis of european and global data. The European Physical Journal Plus, 136:562.
Wallard, H. (2015). Using explained variance allocation to analyse importance of predictors. In Proceedings of the 16th Conference of the Applied Stochastic Models and Data Analysis, Le Pirée, Greece.
Wallard, H. (2019). Grouping property and decomposition of explained variance in linear regression. In Skiadas, C. & Bozeman, J., editors, Data Analysis and Applications 1: Clustering and Regression, Modeling-estimating, Forecasting and Data Mining, pages 73–89. Wiley.
Weber, R. J. (1988). Probabilistic values for games. In The Shapley Value, pages 101–120. Cambridge University Press, 1st edition.
Wei, P., Lu, Z., & Song, J. (2015). Variable importance analysis: a comprehensive review. Reliability Engineering & System Safety, 142:399–432.
Zhao, K. & Hastie, T. (2021). Causal Interpretations of Black-Box Models. Journal of Business & Economic Statistics, 39(1):272–281.
Zou, H. & Hastie, T. (2005). Regularization and Variable Selection via the Elastic Net. Journal of the Royal Statistical Society. Series B (Statistical Methodology), 67(2):301–320.

This work is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.
Copyright (c) 2025 Bertrand Iooss, Laura Clouvel, Vincent Chabridon, Marouane Il Idrissi, Frédérique Robin